
制御が安定しないのはPWMのせい?
分解能シミュレーション方法
デジタル制御ではPWM分解能が制御に大きく影響を与えます。
この記事では、PWMの分解能が与える影響と、そのシミュレーション方法について解説します。
シミュレーションは、パワエレ向け高速回路シミュレータ Scideamで行います。
分解能の計算方法
一般的なマイコンでは、PWMの分解能はスイッチング周波数割るクロック周波数となります。
例えば、TI社のTMS320F28069というマイコンでは、クロック周波数が90MHzですので、100kHzのスイッチングを行うと分解能は
$$\frac{90MHz}{100kHz} = 900$$
となります。
ただし、アップカウンタのみでPWMを作った場合です。アップダウンカウンタを使った場合には、この半分の分解能になります。
(念のために、このマイコンは高分解能PWMを持っていますが、ここでは考慮しません。)
ということで、この分解能をDutyに当てはめましょう。
分解能の適用
PWMの時比率Dutyが0~1の浮動小数点であるとき、以下のプログラムで分解能を適用させることができます。
D = int(Duty * 900) / 900Dは最終的にPWMにセットされる量子化誤差を含む時比率、
int関数は、固定小数点化する関数です。
以上のような式を通すと、浮動小数点Dutyを分解能900倍し、そのうち小数点になってしまったところをint関数で整数化することで小数点を削除し、900で割ることで、分解能を考慮した0~1の値に変換します。
分解能の影響シミュレーション
シミュレーションには、バッテリーにへの充電電流を制御する、デジタル制御による降圧型コンバータを例に挙げてシミュレーションします。
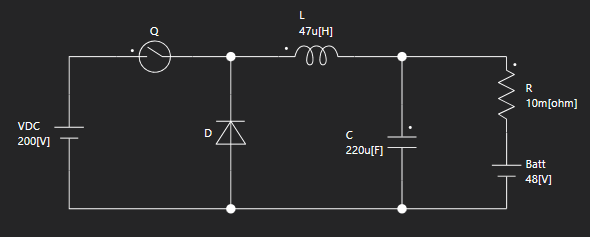
制御系はプログラムで記述しており、量子化誤差の有り無しについて切り替えた結果を確認します。
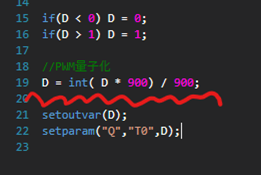
量子化誤差の影響を反映させたくないときは、この一文をコメントアウトすることで簡単に浮動小数点に切り替えることができます。
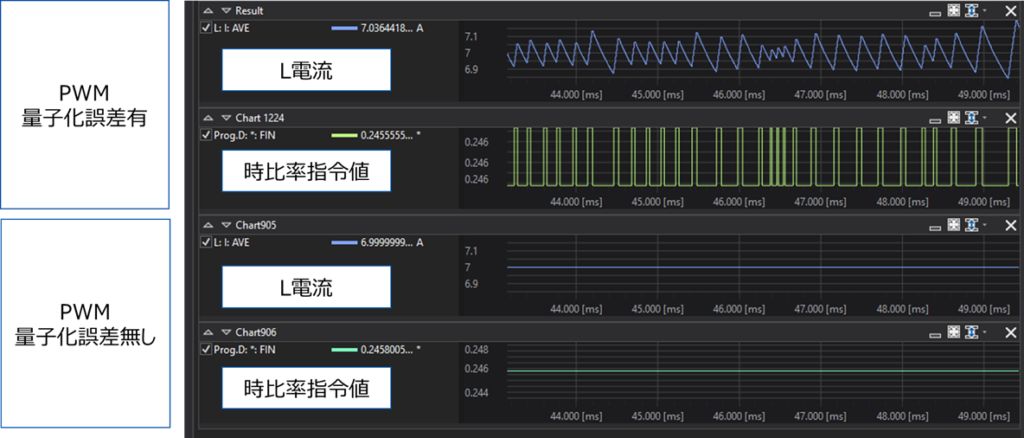
制御系は全く同じですが、PWM量子化誤差がある場合は、およそ0.2Ap-pのリップルがあり、出力は安定しません。
一方、量子化誤差無しの場合は、とても安定しています。
まとめ
PWM分解能が制御系に大きく影響を与えることがよくわかると思います。
もちろん制御系の性能によって分解能の影響を受けにくくるすことも可能ですので、制御実装の前に、是非一度サイディームでシミュレーションしてみてください。
本モデルは、パワエレ向け高速回路シミュレータ Scideamで動作可能です。
本記事のモデルは以下からダウンロードしてください。


