
DABコンバータのシミュレーション
今回はDABコンバータ回路、 Dual Active Bridge (DAB )回路について、簡単な解説とScideamを使ったシミュレーションを行います。
DABコンバータ回路は絶縁型で双方向の電力変換が可能であり、従来の双方向チョッパー回路と絶縁回路を接続した双方向コンバータ回路と比べると回路構成を少なくでき、またソフトスイッチングも行うことができるという特徴を持っています。このような理由から、主に新エネルギーシステムや電気自動車、マイクログリッドなどの分野での用途が期待されています。
本記事から、シミュレーション可能なサンプル回路モデルもダウンロード可能ですので、是非ご利用ください。
それでは始めましょう。
目次
DABコンバータとは
DAB(Dual Active Bridge)コンバータとは絶縁型双方向DC/DCコンバータの一種で、変圧器の一次側と二次側にブリッジ回路を設けた回路です。
DABコンバータの特徴
DABコンバータは以下のような特徴を持つ回路となります。
- 基準相と制御層の位相を変化させることで、双方向の電力変換を行うことができる
- ZVS(Zero Voltage Switching)が可能であり、サージ電圧を小さくできる
これらの特徴から、主に電圧と電流が大きい大容量の電源回路に用いられます。
位相差による電力変換の動作原理
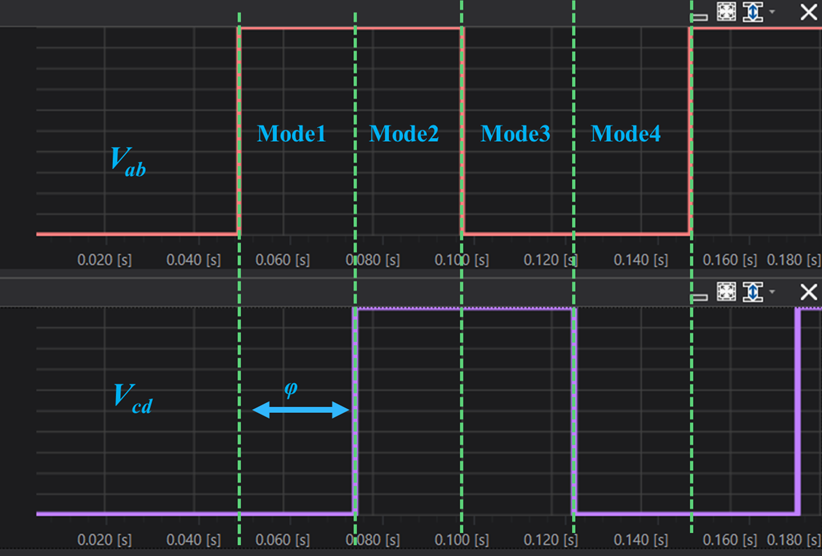
DABコンバータには大きく分けて4つの動作モードがあります。
例えば図1のような回路の場合、一次側から二次側への電力送電を行う場合、図2に示すようにモードが変化します。
なお、図2の $\varphi$ は位相差を表しています。
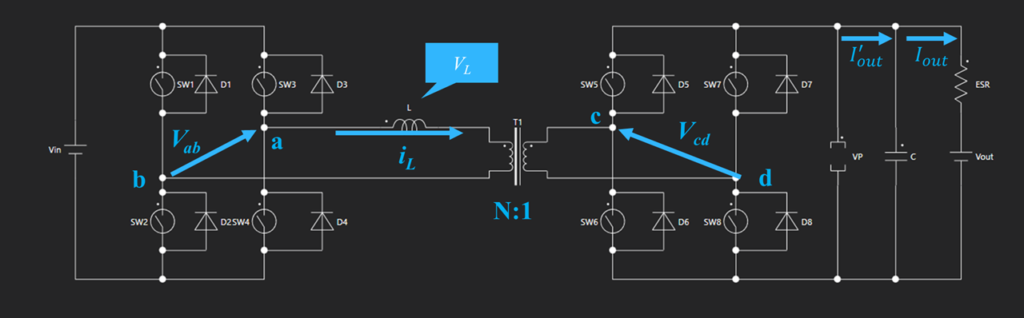
Mode1
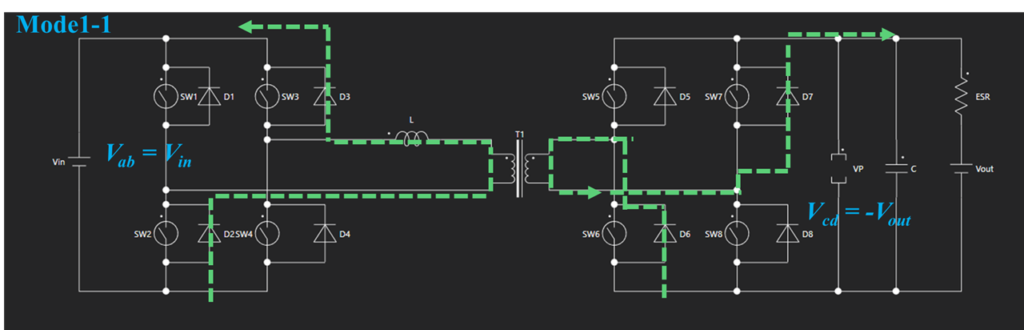
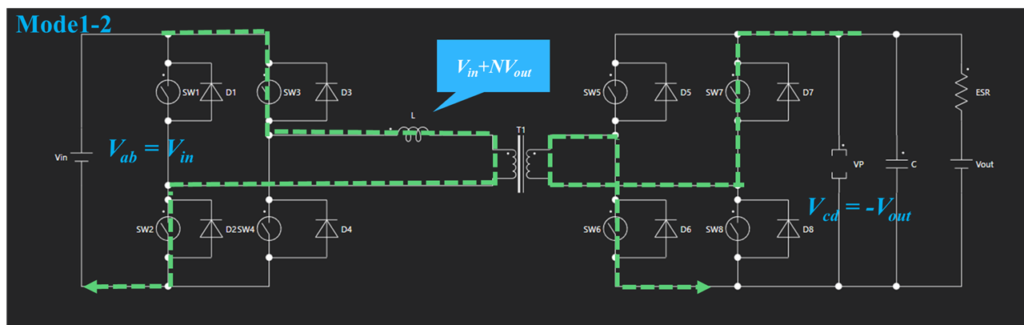
Mode1ではスイッチSW2、SW3、SW6、SW7がオンとなっており、一次側のリアクタンスLに掛かる電圧は $V_{in}+NV_{out}$ となります。
Mode1ではターンオンの前に、直前のModeでリアクタンスLに流れていた電流がボディダイオードを通じて流れるため、Mode1-1のような電流経路を経たあと、Mode1-2のような電流経路となります。
この時$i_L$は次の式で表されます。
$$ i_L = \frac{V_{in} + NV_{out}}{L} t+I_0 \tag{1}$$
$I_0$ : $i_L$の初期値
$t$ : 時間
Mode1は $t=\varphi_d T_s$ まで続き、その後Model-2へと遷移します。
$\varphi_d$ : 位相差 $\varphi$ を正規化した位相シフトデューティ ($\varphi_d=\frac{\varphi}{360}$)
$T_s$ : 周期
Mode2
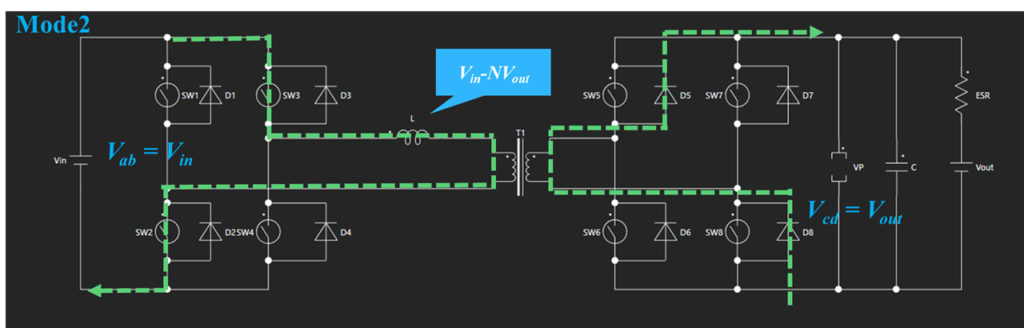
Mode2ではスイッチSW2、SW3、SW5、SW8がオンとなり、一次側のリアクタンスLに掛かる電圧は $V_{in}-NV_{out}$となります。
この時$i_L$は次の式で表されます。
$$ i_L = \frac{V_{in} – NV_{out}}{L} (t-\varphi_d T_s)+I_1 \tag{2}$$
$I_1$ : Mode2開始時の$i_L$
Mode2は$t=0.5T_s$まで続き、その後Mode3へと遷移します。
Mode3
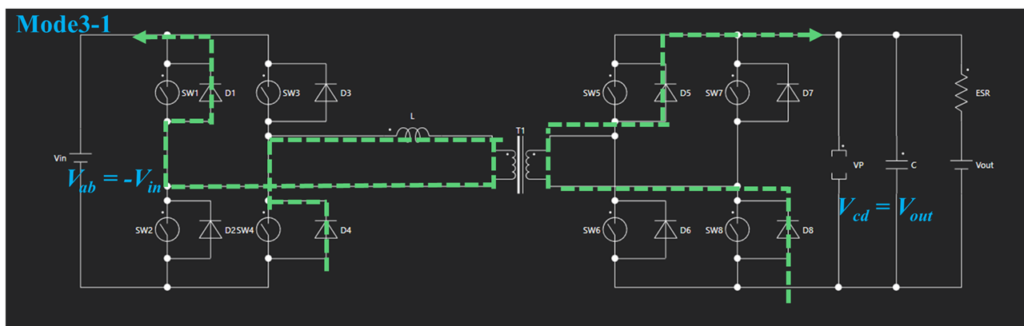
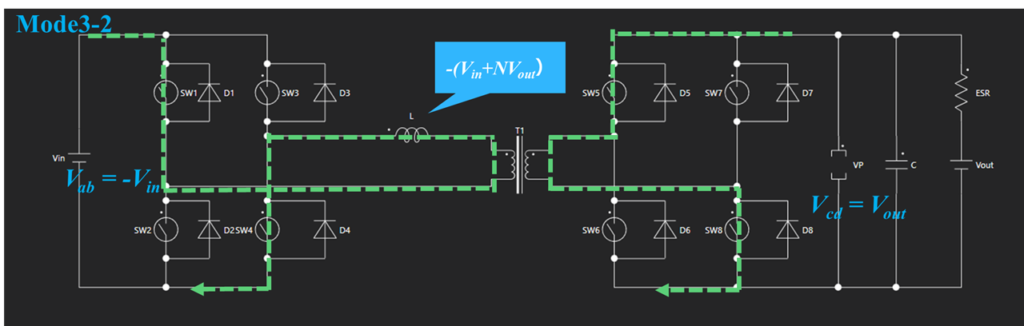
Mode3ではスイッチSW1、SW4、SW5、SW8がオンとなり、一次側のリアクタンスLに掛かる電圧は $-(V_{in}+NV_{out})$ となります。
この時 $i_L$ は次の式で表されます。
$$ i_L = \frac{-(V_{in} + NV_{out})}{L} (t-0.5T_s)+I_2 \tag{3}$$
$I_2$ : Mode3開始時の$i_L$
Mode3は$t=(0.5+\varphi_d)T_s$まで続き、その後Mode4へと遷移します。
Mode4
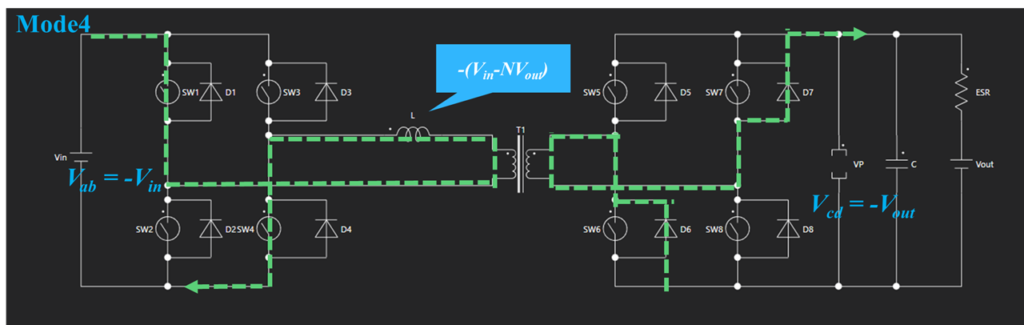
Mode4ではスイッチSW1、SW4、SW6、SW7がオンとなり、一次側のリアクタンスLに掛かる電圧は$-(V_{in}+NV_{out})$となります。
この時 $i_L$ は次の式で表されます。
$$ i_L = \frac{-(V_{in} + NV_{out})}{L} \{ t-(0.5+\varphi_d)T_s \}+I_3 \tag{4}$$
$I_3$ : Mode4開始時の$i_L$
以上のように$i_L$に流れる電流は位相差$\varphi$によってコントロールすることができます。
一次側から二次側へ電力送電を行う場合、各モードにおける$i_L$は図9のようになります。
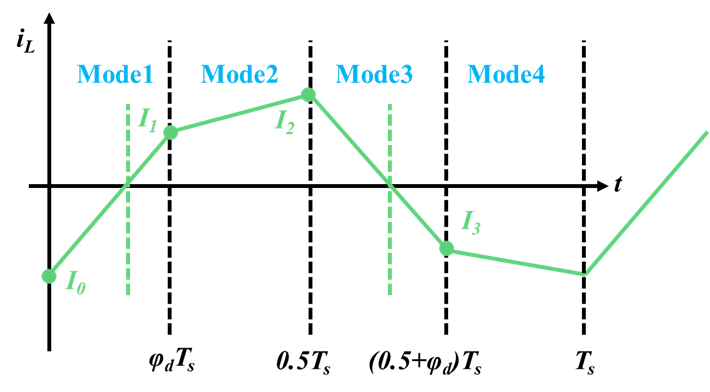
I0、I1、I2、I3は各Modeの電流初期値を示しています。
図9より、動作の対称性から電流初期値は次のような関係を持ちます。
$$I_1=-I_3 \tag{5}$$
$$I_2=-I_0 \tag{6}$$
式(5)、式(6)と図9から、Mode1からMode2までと、Mode3からMode4までの電流$i_L$には対称性があることがわかります。
更に、図1中の出力電流$I’_{out}$は、二次側のコンデンサCの電荷Qに対して、Mode1からMode2までの電荷量から導出することが可能となります。
図3、図4、図5の電流経路と、Mode1-1、Mode1-2、Mode2の各電荷をQ1、Q2、Q3とすれば、$I’_{out}$は次の式で導き出されます。
$$I’_{out} = \frac{Q_1-Q_2+Q_3}{0.5T_s} = \frac{V_{in} T_s \varphi_d(1-2\varphi_d)}{L} \tag{7}$$
DABコンバータでは一次側から二次側への電力送電だけでなく、二次側から一次側への電力送電も可能です。
$$I’_{out} = \frac{V_{in} T_s \varphi_d|1-2\varphi_d|}{L} \tag{8}$$
式(8)から$-0.25<\varphi_d<0.25$の区間では$|\varphi_d|$と共に伝送電力は増加することがわかります。
ZVSが可能な領域と位相シフトデューティの関係について
ZVSの達成条件は次の二点となります。
- スイッチオフ直前の電流はDrainからSourceに流れていること
- スイッチオン直前の電流はSourceからDrainに流れていること
上記を図7の電流初期値で表すと$I_1>0$、$I_2>0$となればZVSが可能です。
$I_1$は式(1)の$iL$における$t$ が$t =\varphi_d$の時の値となるので次のように表せます。
$$I_1 = \frac{V_{in}+NV_{out}}{L}\varphi_d T_s + I_0 \tag{9}$$
同様に$I_2$は式(2)における$t$が$t = 0.5T_s$となった時の値ですので次のように表せます。
$$I_2 = \frac{V_{in} – NV_{out}}{L}(0.5 – \varphi_d) T_s + I_1 \tag{10}$$
式(5)、式(6)の関係から、$I_1$は次のような式に変形することができます。
$$I_1 = \{V_{in} \left( \varphi_d – \frac{1}{4} \right) + \frac{NV_{out}}{4}\}\varphi_d T_s \tag{11}$$
ZVSの条件から$I_1>0$として、入出力電圧比$M$の形に変形させると次の式となります。
$$ M = \frac{NV_{out}}{V_{in}} \ge 1-4\varphi_d \tag{12} $$
同様に$I_2> 0$ となる入出力電圧比 $M$ は次の式で示すことができます。
$$ M = \frac{NV_{out}}{V_{in}} \le \frac{1}{1-4\varphi_d} \tag{13} $$
式(12)と式(13)より、ZVSが可能となる領域は図10のようになります。
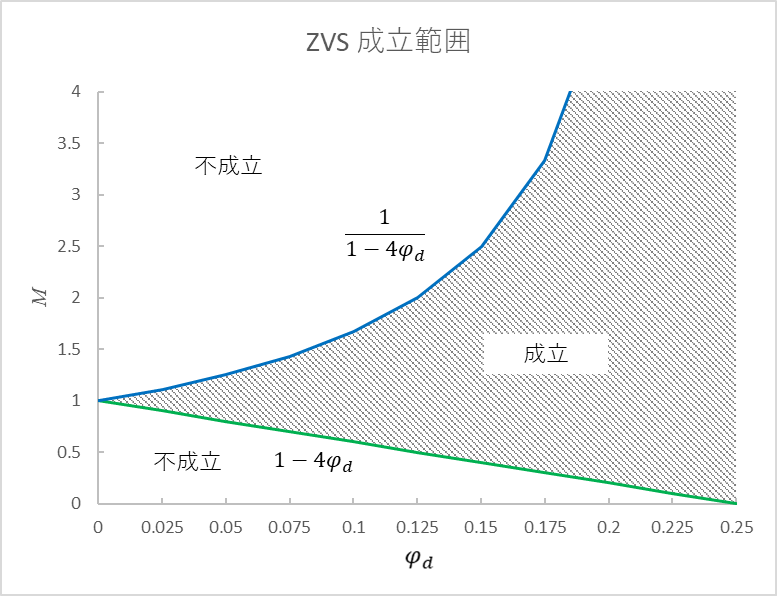
図10より、位相シフトデューティ$\varphi_d$が大きくなるほど、領域が拡大することがわかります。ただし、$|\varphi_d|$を大きくすると、循環電流が増加し、無効電力が増加してしまうので注意が必要となります。そのため、$\varphi_d$の範囲を最も広く取れる$M=1$となるように、変圧器の巻線Nを決定することが重要となってきます[1]。
更に詳しくDABコンバータの解説が知りたい方は、以下の書籍がお勧めです。
平地 克也, “DC/DCコンバータの基礎から応用まで“, 電気学会 (2018), ISBN 9784886863119
また、著者の平地先生のブログにもDABコンバータの解説があります。こちらもご参考にしてください。本記事下部の参考文献よりリンクされています。
シミュレーション
それでは実際にDABコンバータの動きをシミュレーションしてみましょう。
シミュレータはScideam(サイディーム)を使用し、サンプルモデルは本文最後からダウンロード可能です。
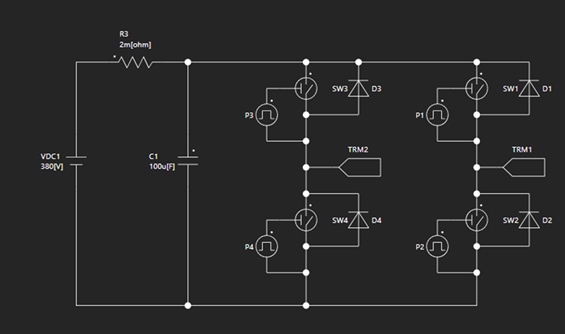
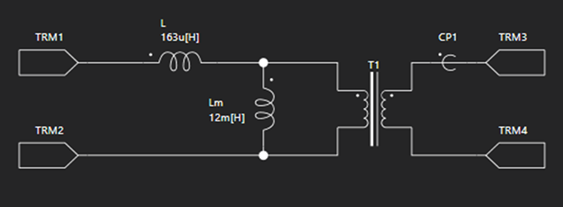
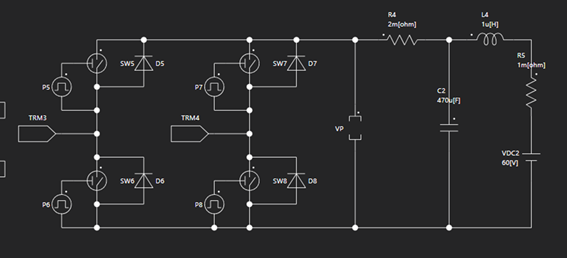
サンプル回路ではスイッチのオンオフをパルス発生器素子と、プログラムによって制御しています。サイディームでは、このような複雑なスイッチングも簡単に構成することが可能です。
サンプル回路では、位相差をプログラム内のSwPhaseで設定しております。こちらで位相を変更していただくことで、位相差による電力送電の変化を確認することができます。(位相は0° < SwPhase < 175°の範囲で変更してください。)
サイディームでのプログラムの使い方は以下のチュートリアルをご覧ください。
上記を踏まえた上で早速、サンプル回路をシミュレーションしてみましょう。
Waveform解析で10[msec]シミュレーションしてみてください。
シミュレーションの結果、図14のような波形が得られます。
位相シフトをされたスイッチの動作や、その時のModeの切り替わりを確認することができます。
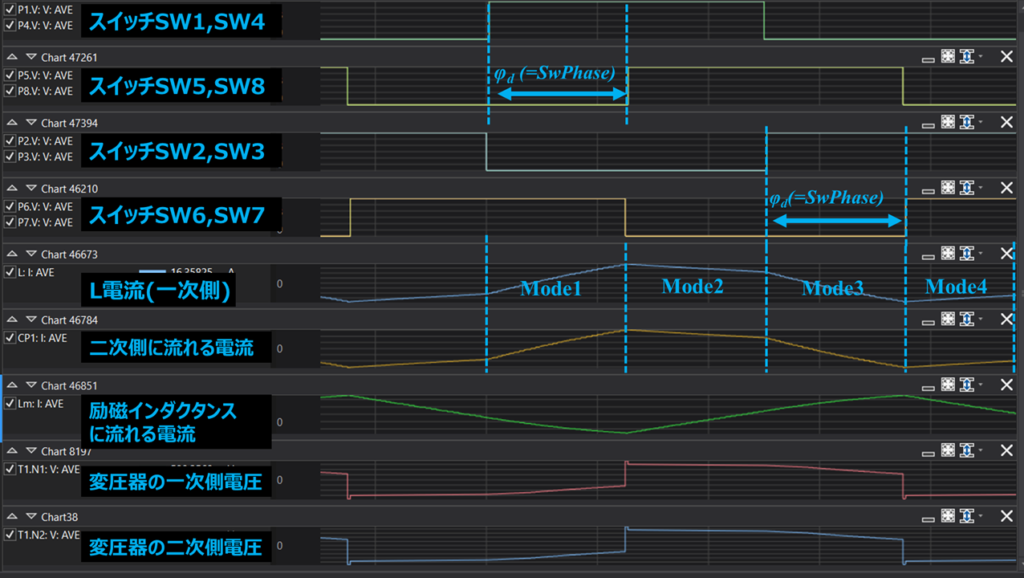
(本回路パラメータは、参考文献[2]をもとに作成しています。)
まとめ
- DABコンバータとは絶縁型双方向DC/DCコンバータの一種で変圧器を挟んで2つのフルブリッジ構造を持つ回路である。
- 位相差によって、電力送電の方向をコントロールすることができる。
- ZVSが可能で、サージ電圧を小さくできる。
- 上記の特徴から主に電圧と電流が大きい大容量の電源回路で使用される
今回はDABコンバータについてのサンプル回路を紹介しました。
スイッチの制御プログラム等を確認・変更して頂き、波形の変化を確認することで、
より回路の動作が深まりますので是非お試しください。
本モデルは、電源パワエレ向け高速回路シミュレータ Scideamで動作可能です。
本記事のモデルは以下からダウンロードしてください。
本文監修:中原正俊、中村創一郎
参考文献
[1]平地 克也, “DC/DCコンバータの基礎から応用まで“, 電気学会 (2018), ISBN 9784886863119
[2]宅間, 比嘉, 伊東, “電圧および負荷運転範囲に着目した 双方向絶縁形 DC-DC コンバータトポロジーの比較検討“
その他、以下のホームページ、動画もお勧めです。
平地研究室技術メモ:DAB 方式双方向 DC/DC コンバータ
茨城大学パワーエレクトロニクスIbaraki Power Electronics:【パワエレ】Dual Active Bridge (DAB)コンバータの基礎 Fundamentals of DAB Converter(Youtube動画)



