いまさら聞けないデジタル電源超入門　
第５回　デジタルフィルタ編

デジタル電源超入門 第４回では、PWMの動作について解説しました。
第５回では、デジタルフィルタについて解説させて頂きます。

フィルタとは

フィルタとはいろいろな周波数の信号が混ざっている信号から、ある範囲の周波数の信号だけ取り出すときに使われます。
家庭の換気扇を考えてみますと、換気扇のフィルタはゴミや汚れをそこでストップさせ、きれいな空気だけを通します。

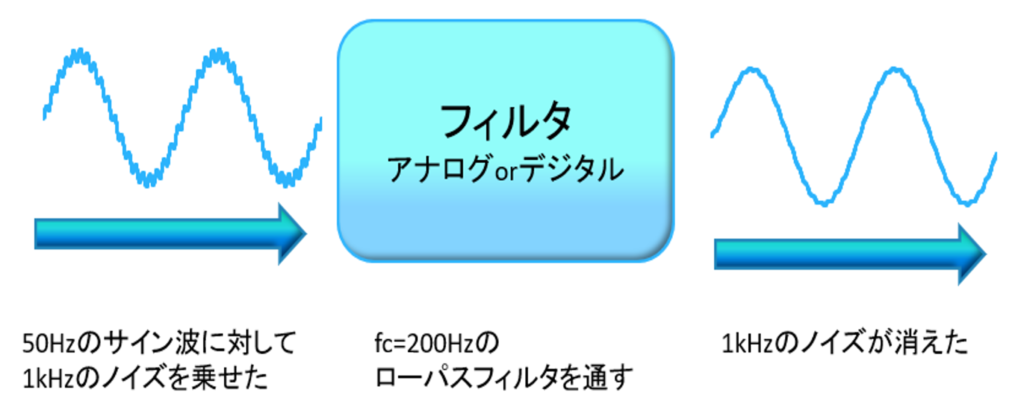
例えば【図１】のように、50Hzの信号の上に1kHzのノイズが乗った信号があるとします。

200Hz以上の信号をカットするローパスフィルタを通すと、1kHzの信号が消え、50Hzの信号だけを取り出すことができます。

デジタル電源では、プログラムの中でデジタルフィルタを使って制御を行います。
そのため今回は、デジタルフィルタについて解説します。

ローパスフィルタ

アナログフィルタの回路は非常に簡単で、抵抗とコンデンサで作ることができます。
それではまず最初に、ローパスフィルタについて解説します。

アナログローパスフィルタは【図２】のような回路構成および周波数特性になっています。

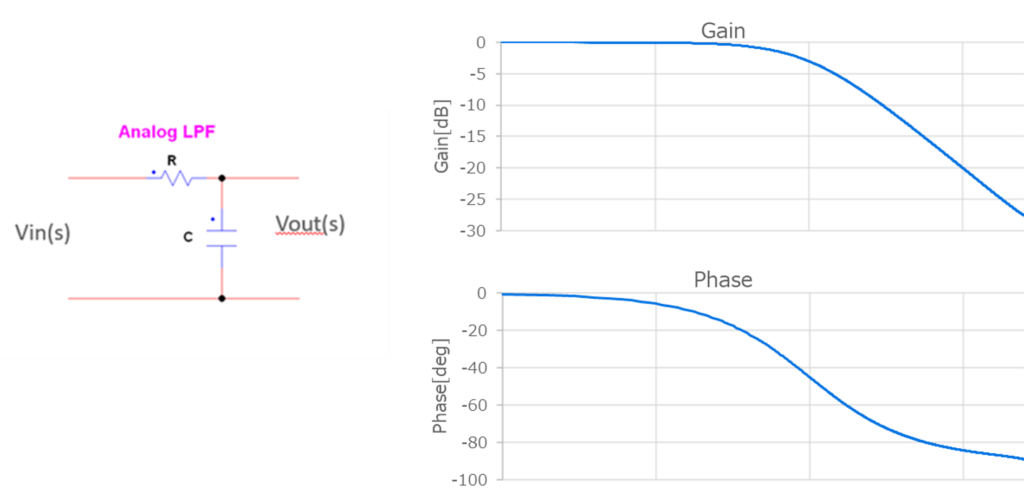
ローパスフィルタの伝達関数は

$$ G(s) = \frac{\frac{1}{CR}}{s+\frac{1}{CR}}=\frac{a}{s+a} $$

となります。

$$ a= 2πf_c $$
$$ f_c ：カットオフ周波数 $$

さて、このアナログローパスフィルタをデジタルに変換するには、フィルタをアナログの
$s$平面から$z$平面に変換する必要があります。

$$ s =\frac{2}{T}\frac{Z-1}{Z+1} $$

を伝達関数に代入することにより、デジタルフィルタの一般形に変換することができます。
これを双一次変換と言います。

それでは双一次変換を行ってみましょう。

$$ G(s) = \frac{a}{s+a} =\frac{a}{\frac{2}{T}\frac{Z-1}{Z+1}+a} $$
$$ A = \frac{2}{T×a} =\frac{1}{T×f_c×π} $$
$$ T : サンプリング周期 $$

とすると

$$ G(s) = \frac{Z+1}{(A+1)Z-A+1} $$

ここで入力を$x$、出力を$y$とすると、

$$ (A+1)y+(-A+1)y_0= x+x_0 $$

$x_0$、$y_0$は、一つ前の入力出力となります。
これを$y$についてまとめると、

$$ y= \frac{1}{A+1}(x+x_0+(A-1)y_0) $$

となります。

Scideamによるローパスフィルタのシミュレーション

それではScideamを使って、ローパスフィルタのシミュレーションを行ってみましょう。

Scideamを立ち上げ、FileからLPF.sファイルを開くと、【図３】のアナログローパスフィルタの回路が表示されます。

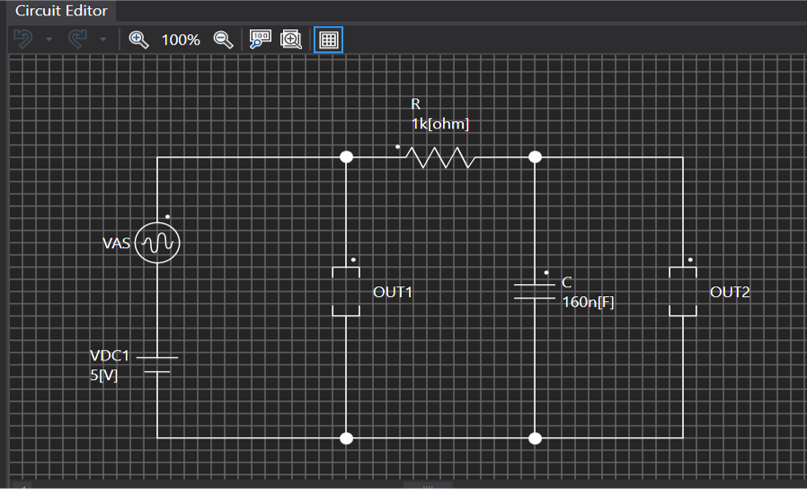
それでは、デジタルフィルタのプログラムを見てみましょう。

画面上部のScriptアイコンをクリックした後、画面右にスクリプト・エクスプローラにあるDigitalLPFをダブルクリックすると、【図４】のプログラムが表示されます。

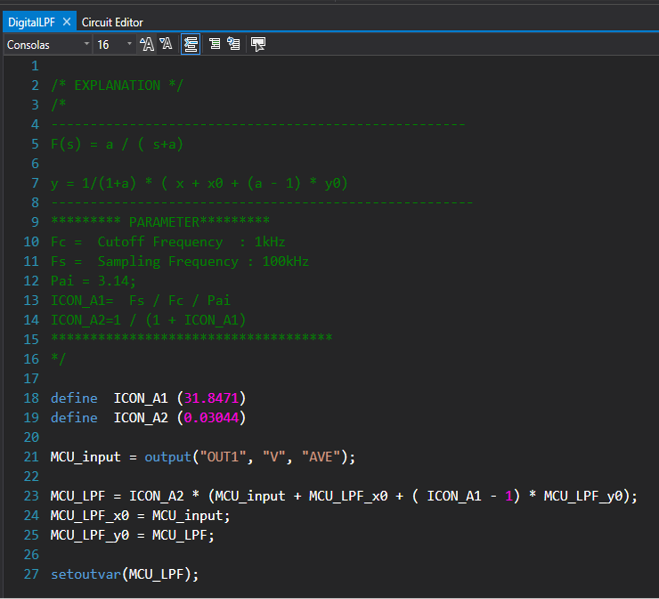
サンプリング周波数　$f_s$=100kHz、カットオフ周波数　$f_c$=1kHzでパラメータを計算すると、
下図のようになります。

それでは、シミュレータを実行させてみましょう。

Scideamではアナログフィルタ回路とデジタルフィルタ・プログラムを同時にシミュレーションして表示できます。

画面上部でWaveformを選び実行すると、【図５】のようなチャートが表示されます。
出力画面を切り替えて、アナログフィルタとデジタルフィルタの出力を確認してください。

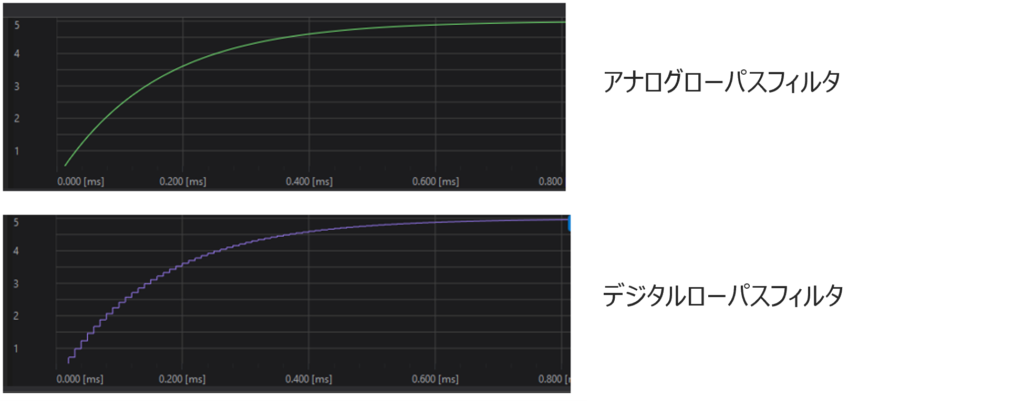
このように、アナログフィルタをデジタルフィルタで再現できることが確認できます。

演習

プロセッサのサンプリング周波数を100kHzから10kHzに変更した時の、デジタルローパスフィルタの動作を確認してみましょう。

Circuit Editorの画面で画面右側のコンフィグに選び、サブ周波数を100kHzから10kHzに変更します。

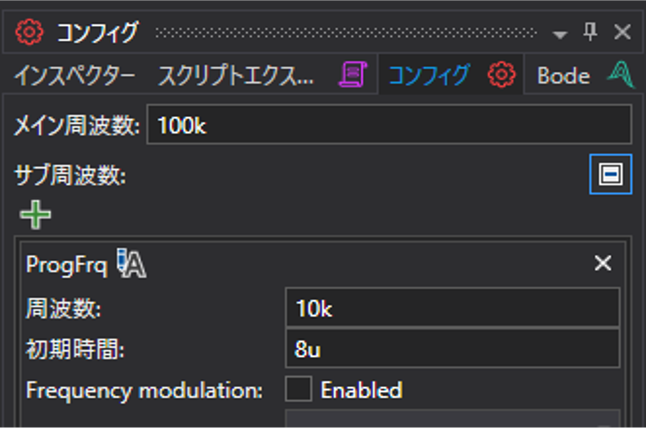
サンプリング周波数の変更に伴い、プログラムのパラメータを下記の様に変更します。

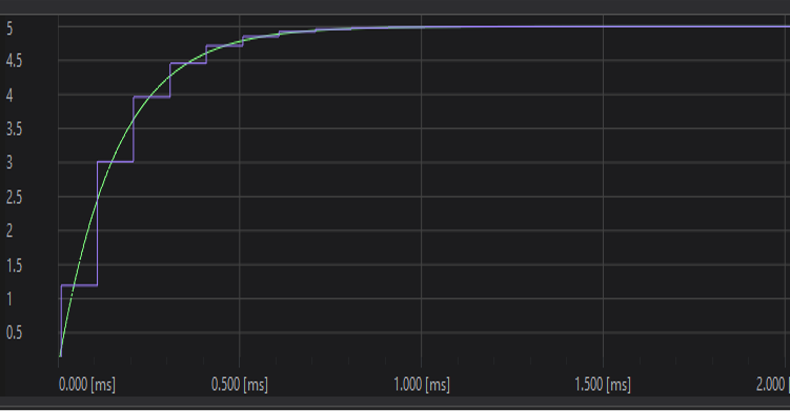
実行ボタンをクリックして、シミュレーションを実行すると、【図６】の結果が得られます。

このチャートを見ると、サンプリング周波数が低いと、アナログフィルタと同じ特性が得られず、デジタルフィルタでアナログフィルタを近似できなくなることが分かります。

ハイパスフィルタ

ローパスフィルタと同様に、ハイパスフィルタの回路構成周波および数特性は【図７】のようになります。

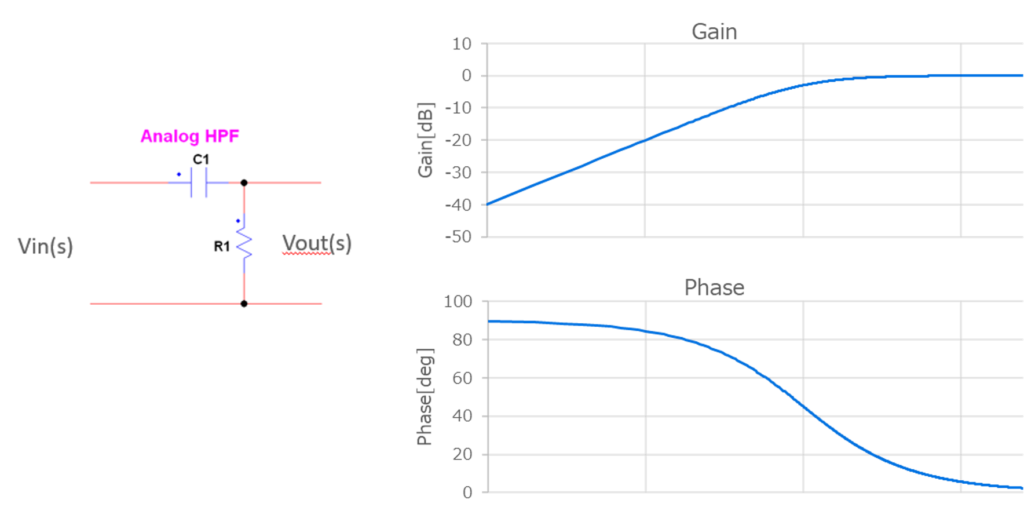
ハイパスフィルタの伝達関数は

$$G(s) = \frac{s}{s+\frac{1}{CR}} = \frac{s}{s+a} $$

となります。

$$ a= 2πf_c $$
$$ fc ：カットオフ周波数 $$

$$s = \frac{2}{T} \frac{Z-1}{Z+1} $$

を代入すると

$$G(s) = \frac{ \frac{2}{T} \frac {Z-1}{Z+1}}{ \frac{2}{T} \frac{Z-1}{Z+1}+a} = \frac{2(Z-1)}{2(Z-1)+aT(Z+1)} $$

$$ A = \frac{2}{T\times a} = \frac{1}{T×f_c×π} $$
$$ T : サンプリング周期 $$

とすると

$$G(s) =\frac{A(Z-1)}{A(Z-1)+(Z+1)} $$

$$G(s) = \frac{AZ-A}{(A+1)Z+-A+1} $$

最終的に
$$y = \frac{1}{1+\frac{1}{A}}(x-x_0+(1-\frac{1}{A})y_0)$$

となります。ここで$x_0$、$y_0$は、ひとつ前の入力および出力となります。

それではScideamで、ハイパスフィルタのシミュレーションを行ってみましょう。

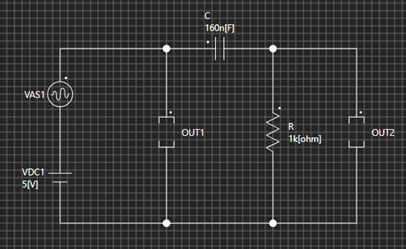
Scideamを立ち上げ、ダウンロードしたHPF.sファイルを開きます。
【図８】のような回路となります。

次に、画面上部のスクリプト・アイコンをクリックして、
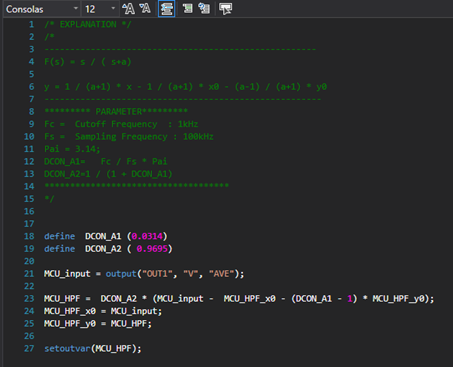
画面右側のスクリプト・エクスプローラでDigitalHPFをダブルクリックすると、
画面中央に【図９】のプログラムが表示されます。

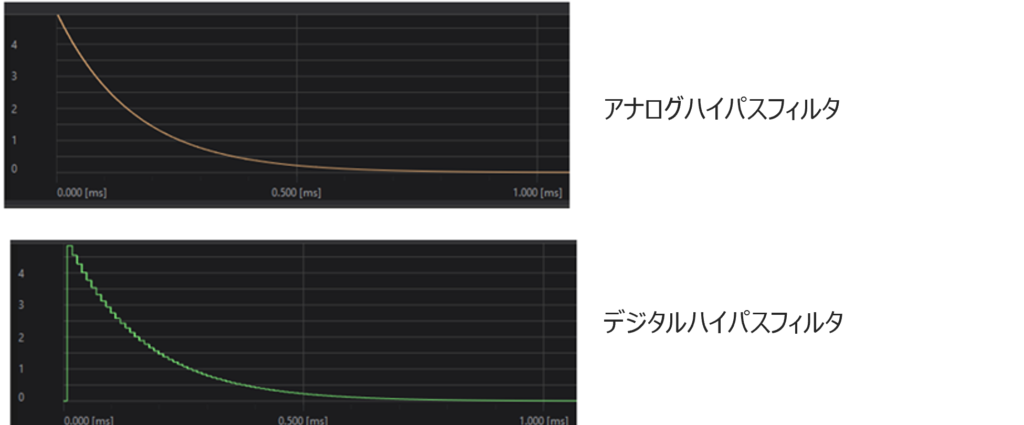
Waveformを選択して実行すると、【図１０】のチャートが表示されます。
画面ではアナログとデジタルを切り替えて表示されています。

このチャート見ると、アナログハイパスフィルタもデジタルハイパスフィルタで再現できることが分かります。

まとめ

シミュレーション結果でも分かるように、プログラムでデジタルフィルタを再現することができます。
今回シミュレーションした、二つのデジタルフィルタは、次の章で行うデジタル制御で使用します。

次回はいよいよ、デジタル電源の重要な要素である、デジタル制御になります。
今回ご説明したデジタルフィルタが、どのように使われるのか、ご期待ください。

▼関連投稿　ーデジタル電源超入門ー